数据结构 - nixBlog

SGF Tree

试图将SGF文件变成树，简化版本

SGF是一种可以是用于围棋棋谱记录的文本格式，关键的部分大概类似这样：

(;B[cd];W[pq](;B[cq];W[do])(;B[cf];W[pn]))

如果先从简单的模型开始，例如简化成：

(AB(CD)(EF))

要把这样的字符串解析成一棵二叉树（最简单的情况），使用下面的代码：

?
sgf_tree_simple.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#!/usr/bin/env python
# -*- coding: utf-8 -*-
 
def make_node(color='@', left={}, right={}):
    node = {
        'color': color,
        'left': left,
        'right': right
    }
    return node
 
def make_sgf_tree(sgf_str='', index=[0], head=make_node()):
    current_node = head
    # 遍历字符串
    while True:
        index[0] += 1 # 记录字符串被处理的当前位置，技巧：参数修改
        # 循环退出条件
        if sgf_str[index[0]] == ')':
            break
        # 递归处理内层的括号对
        elif sgf_str[index[0]] == '(':
            make_sgf_tree(sgf_str, index, current_node)
        # 非括号字符作为节点的color
        else:
            n = make_node(color=sgf_str[index[0]])
            # 尽量插在树的右边
            if not current_node['right']:
                current_node['right'] = n
            elif not current_node['left']:
                current_node['left'] = n
            else:
                print 'should NOT be there....'
            current_node = n
 
# 前序遍历
def tree_pre_trav(head=make_node()):
    start = head
    if not start:
        return
    print start['color'],
    tree_pre_trav(start['left'])
    tree_pre_trav(start['right'])
 
# 后序遍历
def tree_post_trav(head=make_node()):
    start = head
    if start['left']:
        tree_post_trav(start['left'])
    if start['right']:
        tree_post_trav(start['right'])
    print start['color'],
 
# 中序遍历
def tree_in_trav(head=make_node()):
    start = head
    if start['left']:
        tree_in_trav(start['left'])
    print start['color'],
    if start['right']:
        tree_in_trav(start['right'])
 
if __name__=='__main__':
    # sgf_str = '(B(W(BW)(BWB))(WBW))'
    sgf_str = '(A(B(CD)(EFG))(HIJ))'
    print 'SGF String: \"' + sgf_str + '\"'
    sgf_str_index = [0]
    head = make_node()
 
    make_sgf_tree(sgf_str=sgf_str, index=sgf_str_index, head=head)
    print '\nThe SGF Tree:'
    print head
    print '\nPreorder Traversal:'
    tree_pre_trav(head)
    print '\n\nPostorder Traversal:'
    tree_post_trav(head)
    print '\n\nInorder Traversal:'
    tree_in_trav(head)

输出：

?
sgf_tree_simple.py 输出
1
2
3
4
5
6
7
8
9
10
11
12
13
SGF String: "(A(B(CD)(EFG))(HIJ))"
 
The SGF Tree:
{'color': '@', 'right': {'color': 'A', 'right': {'color': 'B', 'right': {'color': 'C', 'right': {'color': 'D', 'right': {}, 'left': {}}, 'left': {}}, 'left': {'color': 'E', 'right': {'color': 'F', 'right': {'color': 'G', 'right': {}, 'left': {}}, 'left': {}}, 'left': {}}}, 'left': {'color': 'H', 'right': {'color': 'I', 'right': {'color': 'J', 'right': {}, 'left': {}}, 'left': {}}, 'left': {}}}, 'left': {}}
 
Preorder Traversal:
@ A H I J B E F G C D
 
Postorder Traversal:
J I H G F E D C B A @
 
Inorder Traversal:
@ H I J A E F G B C D

应该就是下图的样子：

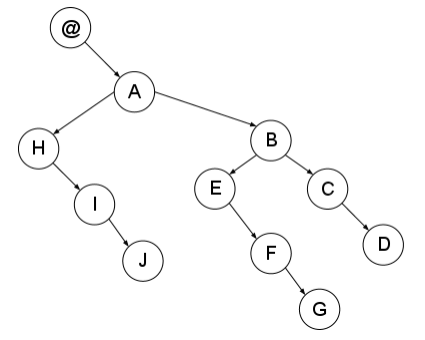
SGF Tree

 

 

 

 

 

 

 

 

 

 

 

 

其实最后得到的代码，不过是将一个表示二叉树的字符串变成一颗二叉树而已。再稍微扩展一下，应该就能解析SGF文件了。再然后，就可以设计一个围棋打谱程序了。

还有一个我之前写的C语言的版本，指针与二叉树，可能适合C语言的思维：

 

?
sgf_tree.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <stdio.h>
#include <stdlib.h>
 
struct node {
    char color;
    char x;
    char y;
    struct node *left;
    struct node *right;
};
 
// record the beginning of sgf string
char *start = NULL;
 
void make_sgf_tree(struct node *head, char *str) {
    start = str;
    struct node *current_node = head;
             
    while (*start != '\n') {
        start += 1;
 
        if (*start == ')')
            break;
        else if (*start == '(')
            make_sgf_tree(current_node, start); // 递归，我们都喜欢
        else {
            if (*start == ';') { // 围棋动作的开始，期望类似 ;W[ab]...
                struct node *new_node = (struct node*)malloc(sizeof(struct node));
                new_node->color = *(start+1);
                new_node->x = *(start+3);
                new_node->y = *(start+4);
                printf("(%c,%c)\n", new_node->x, new_node->y);
                start += 5; //FIXME, there is a better way to parse
 
                if (current_node->right == NULL)
                    current_node->right = new_node;
                else if (current_node->left == NULL)
                    current_node->left = new_node;
                else
                    printf("22not children........\n");
                current_node = new_node;
     
                 
            }
        }
    }
}
 
// 前序遍历
void show_tree_pre(struct node *head)
{
    struct node *start = head;
    if (start != NULL)
        printf("<%c(%c,%c)>\n", start->color, start->x, start->y);
    if (start->left != NULL)
        show_tree_pre(start->left);
    if (start->right != NULL)
        show_tree_pre(start->right);
}
     
int main()
{
    // 简单的测试，sgf文件的子集，且限定成最简单的二叉树（假定某手棋的变化之多有两种）
    char *str = "(;W[ab];B[cd](;W[ef];B[ac](;W[ss];B[rr])(;W[gg];B[hh]))(;W[ee];B[bc]))\n";
    printf("SGF string: %s",str);
 
    // 我们把它变成一颗树
    struct node *head = (struct node*)malloc(sizeof(struct node));
    make_sgf_tree(head, str);
 
    // 再前序遍历看看这个树是不是我们想想的样子
    printf("\npreorder travelsal:\n");
    show_tree_pre(head->right);
 
    return 0;
}

数据结构 python SGF c tree Comments(1) 2012年1月07日 12:06